基础算法

随机变量

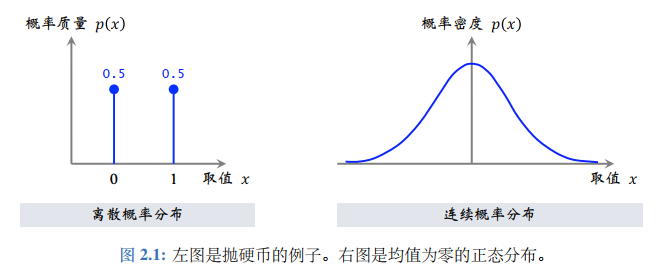
  • 随机变量X： 一个不确定量，取决于一个随机事件的结果。
  • 观测值x： 一个确定量，是一次随机事件的观测结果。
  • 累计分布误差（CDF）： FX(x)=P(X≤x)F_X(x)=\mathbb{P}(X\le x)，FX:R→[0,1]F_X:\mathbb{R}\to[0,1]
  • 概率质量函数（PMF）： 离散概率分布，即变量取值范围χ\chi为离散集合。
    • ∑x∈χp(x)=1\sum_{x\in\chi}p(x)=1
    • h(x)h(x)关于变量XX的期望为EX∼p(⋅)[h(x)]=∑x∈χp(x)⋅h(x)\mathbb{E}_{X\sim p(\cdot)}[h(x)]=\sum_{x\in\chi}p(x)\cdot h(x)
  • 概率密度函数（PDF）： 连续概率分布，即变量取值范围χ\chi为连续集合。
    • ∫−∞xp(u)du=FX(x)\int_{-\infty}^x p(u)du=F_X(x)
    • ∫Rp(x)dx=1\int_\mathbb{R}p(x)dx=1且p(x)=FX′(x)p(x)=F^{'}_X(x)
    • h(x)h(x)关于变量XX的期望为EX∼p(⋅)[h(x)]=∫χp(x)⋅h(x) dx\mathbb{E}_{X\sim p(\cdot)}[h(x)]=\int_{\chi}p(x)\cdot h(x)\:dx

image-20230407145528307

蒙特卡洛示例

估计圆周率

蒙特卡洛方法（Monte-Carlo methods）也被称为统计模拟方法，是一种基于概率统计的数值计算方法。运用蒙特卡洛方法时，我们通常使用重复随机抽样，然后运用概率统计方法来从抽样结果中归纳出我们想求的目标的数值估计。

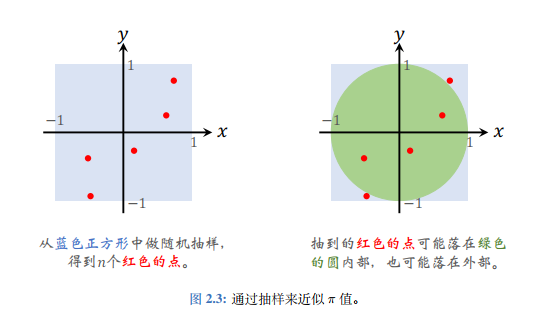
均匀生成n个[−1,1][-1,1]内的随机数坐标，其中落入园内的点的概率为圆面积与正方形面积的比值p=π4p=\frac{\pi}{4}：

image-20230407153823402

设圆内点数量为随机变量MM，则其期望为E[M]=pn=π4⋅n\mathbb{E}[M]=pn=\frac{\pi}{4}\cdot n。在大数定律下，落入圆内点的个数mm将近似于期望值πn4\frac{\pi n}{4}，进而可近似得到圆周率的值π=4mn\pi=\frac{4m}{n}。伪代码如下：

image-20230407172246609

Python代码实现如下：

import numpy as np

def MonteCarloApproximationPi(n):
    # 初始化
    m = 0
    # 在[-1, 1] x [-1, 1]的空间中随机取n个点。
    x_lst = np.random.uniform(-1, 1, size=n)
    y_lst = np.random.uniform(-1, 1, size=n)
    
    for x, y in zip(x_lst, y_lst):
        if x ** 2 + y ** 2 <= 1:
            m += 1
            
    # 近似计算圆周率
    pi = 4 * m / n
    return pi

估计阴影面积

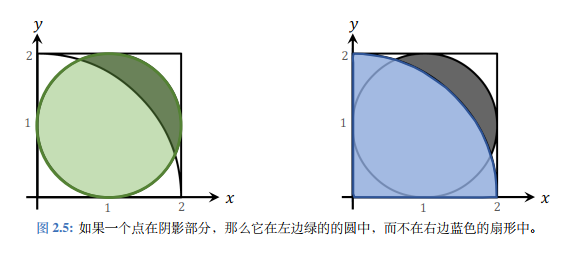
求下图中阴影部分面积可采用蒙特卡洛估计进行，其内圆为圆心(1,1)(1,1)，半径为11的圆，外接边长为22的正方形，则阴影部分处于圆内且不在扇形部分中：

image-20230410162753399

求解思路：若在正方体内均匀采样nn个点，则落入阴影部分的概率为p=a2a1=a24p=\frac{a_2}{a_1}=\frac{a_2}{4}，其中a1a_1表示为正方形面积，a2a_2为阴影面积。若设MM个点落入a2a_2，则期望E[M]=np=na24\mathbb{E}[M]=np=\frac{na_2}{4}；此处观测可知道mm个点落入，则可知a2≈4mna_2 \approx \frac{4m}{n}，伪代码如下：

image-20230410164906010

Python代码实现如下：

import numpy as np

def MonteCarloApproximationShadow(n):
    # 初始化
    m = 0
    # 在[0, 2] x [0, 2]的空间中随机取n个点。
    x_lst = np.random.uniform(0, 2, size=n)
    y_lst = np.random.uniform(0, 2, size=n)

    for x, y in zip(x_lst, y_lst):
        if (x - 1) ** 2 + (y - 1) ** 2 <= 1 and x ** 2 + y ** 2 > 4:
            m += 1

    # 近似计算a_2
    a_2 = 4 * m / n
    return a_2

蒙特卡洛应用

一元定积分估计

I=∫ab f(x) dxI=\int_a^b\:f(x)\:dx

image-20230410171541373

import math
import numpy as np

def MonteCarloApproximationOneVariableDefiniteIntegral(n, a, b, f):
    x_lst = np.random.uniform(a, b, size=n)
    I = (b - a) / n * np.sum(list(map(f, x_lst)))
    return I


if __name__ == "__main__":
    f = lambda x : (1 + math.sin(x) * math.log(x, math.e) ** 2) ** (-1)
    i = MonteCarloApproximationOneVariableDefiniteIntegral(100, 0.8, 3, f)
    print("100个点近似：", i)

    i = MonteCarloApproximationOneVariableDefiniteIntegral(10000, 0.8, 3, f)
    print("10000个点近似：", i)

    i = MonteCarloApproximationOneVariableDefiniteIntegral(1000000, 0.8, 3, f)
    print("1000000个点近似：", i)

多元定积分估计

I=∫Ω f(x) dxI=\int_\Omega\:f(x)\:dx

image-20230410184637900

此处以二元定积分为例进行求解：

image-20230410180206323

import math
import numpy as np

def MonteCarloApproximationDefiniteIntegral(n, omega_x, omega_y, f):
    x_lst = np.random.uniform(omega_x[0], omega_x[1], size=n)
    y_lst = np.random.uniform(omega_y[0], omega_y[1], size=n)

    v = (omega_x[1] - omega_x[0]) * (omega_y[1] - omega_y[0])

    I = v / n * np.sum(list(map(f, zip(x_lst, y_lst))))
    return I


if __name__ == "__main__":
    f = lambda cor : 1 if cor[0] ** 2 + cor[1] ** 2 <= 1 else 0
    i = MonteCarloApproximationDefiniteIntegral(100, (-1, 1), (-1, 1), f)
    print("100个点近似：", i)

    i = MonteCarloApproximationDefiniteIntegral(10000, (-1, 1), (-1, 1), f)
    print("10000个点近似：", i)

    i = MonteCarloApproximationDefiniteIntegral(1000000, (-1, 1), (-1, 1), f)
    print("1000000个点近似：", i)

期望估计

EX∼p(⋅)[f(x)]=∫Ωp(x)⋅f(x) dx\mathbb{E}_{X\sim p(\cdot)}\big[f(x)\big]=\int_{\Omega}p(x)\cdot f(x)\:dx

根据期望密度函数p(x)p(x)采样得到样本xx将使得估计更快收敛，伪代码如下：

image-20230410185214099

为降低内存开销，进一步使用递推式计算上述估计，Robbins-Monro算法思路如下：

image-20230410185157068

import math
import numpy as np

def MonteCarloEstimationExpectation(n, f, omega, alpha):
    # 高斯分布，均值1，标准差2
    i = 0
    q = 0
    while i < n:
        x = np.random.normal(loc=1, scale=2, size=1)
        if omega[0] <= x <= omega[1]:
            q = (1 - alpha) * q + alpha * f(x)
            i = i + 1
    return q

if __name__ == "__main__":

    f = lambda x : 2 * x + 10 * math.sqrt(math.fabs(x)) + 3
    alpha = 0.04

    i = MonteCarloEstimationExpectation(100, f, (2, 8), alpha)
    print("100个点近似：", i)

    i = MonteCarloEstimationExpectation(10000, f, (2, 8), alpha)
    print("10000个点近似：", i)

    i = MonteCarloEstimationExpectation(10000, f, (2, 8), alpha)
    print("1000000个点近似：", i)

动态规划算法

动态规划

将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到目标问题的解。动态规划会保存已解决的子问题的答案，在求解目标问题的过程中，需要这些子问题答案时就可以直接利用，避免重复计算。

  • 最优子结构： 问题的最优解由相关子问题的最优解组合而成，且这些子问题可独立求解
    • 使用动态规划算法时，用子问题的最优解来构造原问题的最优解
  • 重叠子问题： 递归算法反复求解相同子问题，在动态规划算法中使用数组来保存子问题的解，从而通过查表代替重复求解
    • 记录方式主要包括备忘录法（自顶而下）、自底而上
    • 动态规划主要使用底子而上的方式进行求解，从而避免了额外的递归调用开销。

斐波那契数列

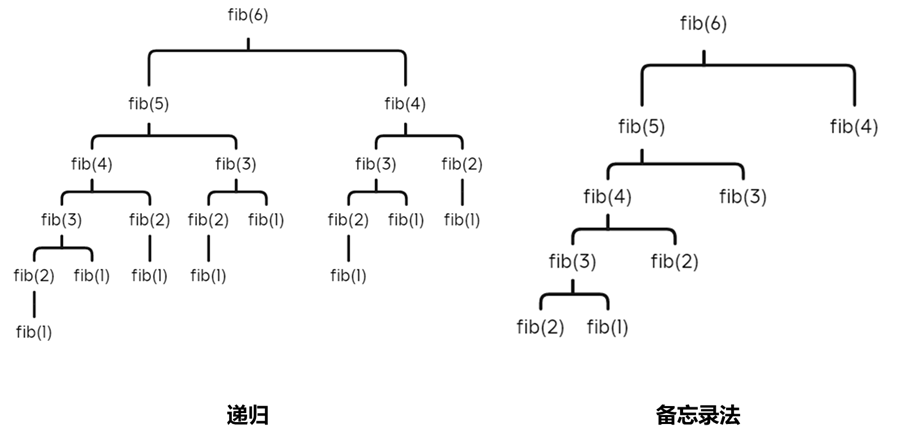
斐波那契数列通过递归调用方式实现：

def fib(n):
    if n <= 0:
        return 0
    elif n == 1:
        return 1
    return fib(n-1) + fib(n-2)

使用备忘录进行自顶而下的求解：

  • memo用于存储斐波那契数列，初始化为-1
  • 若第i项斐波那契数列已经被计算得到，则将被存储至memo[i]中
  • 若调用已被计算得到的第i项斐波那契数列，则直接调取memo[i]而不再递归调用子树
def fibonacci(n):
    if n <= 0:
        return 0
    memo = [-1 for i in range(n)]

    return fib(n, memo)

def fib(n, memo):
    if memo[n-1] != -1:
        return memo[n-1]
    elif n<= 2:
        memo[n-1] = 1
    else:
        memo[n-1] = fib(n-1, memo) + fib(n-2, memo)

    return memo[n-1]

image-20230411154742733

使用动态规划的自底而上思想：

def fib(n):
    memo = [1, 1]
    for i in range(1, n):
        memo.append(memo[i] + memo[i - 1])

    return memo[n-1]

钢条切割问题

给定一段长度为nn英寸的钢条和价目表pip_i，求切割钢条的最优方案使得销售收益rnr_n最大：

image-20230411153613536

问题可被抽象为不断将钢铁切割为两段，每次选取收益最大的方式进行切割：

# 价值表
p_lst = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]

def cut(n):
    if n<= 0:
        return 0
    elif n == 1:
        return 1
    else:
        # 不切割的价值
        r = p_lst[n-1]
        # 切割后的价值
        for i in range(1, n // 2 + 1):
            r = max(r, cut(i) + cut(n-i))
        return r

备忘录版将每一步存储至备忘录中：

# 价值表
p_lst = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]

def cutMemo(n):
    if n <= 0:
        return 0

    memo = [-1 for i in range(n)]

    return cut(n, memo)

def cut(n, memo):
    if memo[n-1] != -1:
        return memo[n-1]
    elif n == 0:
        r = 0
    else:
        # 不切割的价值
        r = p_lst[n-1]
        # 切割后的价值
        for i in range(1, n // 2 + 1):
            r = max(r, cut(i, memo) + cut(n-i, memo))

    memo[n-1] = r
    return memo[n-1]

动态规划则自底而上进行：

# 价值表
p_lst = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
def cut(n):
    r = p_lst[:n]
    for i in range(0, n):
        for j in range(0, i-1):
            r[i] = max(r[i], r[j] + r[i-j-1])
    return r[n-1]

强化学习基础

专有名词

状态与观测

  • 智能体（Agent）： 动作、决策的执行者，被控对象（下棋机器人）
  • 环境（Environment）： 智能体交互的对象（棋盘）
  • 状态（State）： 对当前时刻环境的完备描述，是决策的依据（棋盘上所有棋子的位置）
  • 观测（Observation）： 对当前时刻环境的部分描述，为状态的子集（棋盘上某一棋子附近的信息）
  • 状态空间（State Space）： 所有可能存在状态的集合，记作S\mathcal{S}，状态空间可以是离散或连续的，可以是有限或无限的（下棋的状态空间为离散有限集合）
  • 智能体通过接受观测输出动作和智能体状态，环境接受智能体动作并输出环境状态
    • 强化学习中的状态为环境的状态，而非智能体的状态
    • 完全可观测（Fully Observed）： 智能体观测到的状态和环境的状态等价时，称环境为可观测的，此时可用马尔可夫决策过程（MDP）进行建模环境
    • 部分可观测（Partially Observed）： 智能体的观测不包含环境的所有状态，称环境是部分可观测的，此时建模为可观测马尔可夫决策过程（POMDP）

动作、奖励、状态转移

  • 动作（Action）： 智能体基于当前状态所作的决策，动作的选取可存在随机性（以一定概率选取某一动作）（围棋中361个位置对应361个动作）
  • 动作空间（Action Space）： 所有可能动作的集合，记作A\mathcal{A}，动作空间可以是离散或连续的，可以是有限或无限的（围棋中A={1,2,3,⋯ ,361}\mathcal{A}=\{1, 2, 3,\cdots,361\}）
  • 奖励（Reward）： 智能体执行某一动作后，环境反馈给智能体的一种标量反馈信号
    • 奖励为当前状态ss、当前动作aa、下一刻状态s′s^{'}的函数r(s,a,s′)r(s,a,s^{'})
    • 奖励函数是有界的：∀ a∈A,s,s′∈S,s.j., ∣r(s,a,s′)∣<∞\forall\: a\in\mathcal{A},s,s^{'}\in\mathcal{S},s.j.,\:\begin{vmatrix}r(s,a,s^{'})\end{vmatrix}<\infty
  • 状态转移（State Transition）： 描述智能体从当前时刻tt的状态ss转移至下一时刻状态s′s^{'}的过程
    • 状态转移概率函数（State Transition Probability Function）： 状态转移存在来自于环境的随机性
    • pt(s′ ∣ s)=P(St+1′ ∣ St=s)p_t(s^{'}\:|\:s)=\mathbb{P}\big(S_{t+1}^{'}\:|\: S_t=s\big)表示从当前状态ss下，环境状态转移至s′s^{'}的概率

回合与轨迹

  • 回合（Episode）： 智能体从游戏开始到通关或结束的一次过程，类比监督学习中的Epoch
  • 历史（History）： 历史是观测、动作、奖励的序列，Ht=o1,a1,r1,⋯ ,on,an,rnH_t=o_1,a_1,r_1,\cdots,o_n,a_n,r_n
    • 状态是历史的函数St=f(Ht)S_t=f(H_t)
  • 轨迹（trajectory）： 智能体在一回合中观测到的所有状态、动作、奖励，τ=s1,a1,r1,⋯ ,sn,an,rn\tau=s_1,a_1,r_1,\cdots,s_n,a_n,r_n

image-20230411125003012

马尔可夫过程

MP

  • 马尔可夫性质（Markov Property）： 一个随机过程给定过去状态和当前状态下，未来时刻状态只取决于上一时刻的状态，而与历史无关

P(St+1 ∣ St)=P(St+1 ∣ S1,⋯ ,St)\mathbb{P}(S_{t+1}\:|\:S_t)=\mathbb{P}(S_{t+1}\:|\:S_1,\cdots,S_t)

  • 马尔可夫过程（Markov Process，MP）： 具备马尔可夫性质的随机过程称为马尔可夫过程

  • 马尔可夫链（Markov Chain）： 离散时间的马尔可夫过程称为马尔科夫链，用元组<S,P><\mathcal{S},\mathcal{P}>表示

    • 马尔可夫链是最简单的MP，其状态是有限的

  • 状态转移矩阵（State Transition Matrix）：用于描述马尔科夫链中的状态转移p(St+1=s′ ∣ St=s)p(S_{t+1}=s^{'}\:|\:S_t=s)

    • p(si ∣ sj)p(s_i\:|\:s_j)表示从sjs_j转移至sis_i的概率
    • 从某个状态转移至其他状态的概率和为1，即P\mathcal{P}的每一行和为1

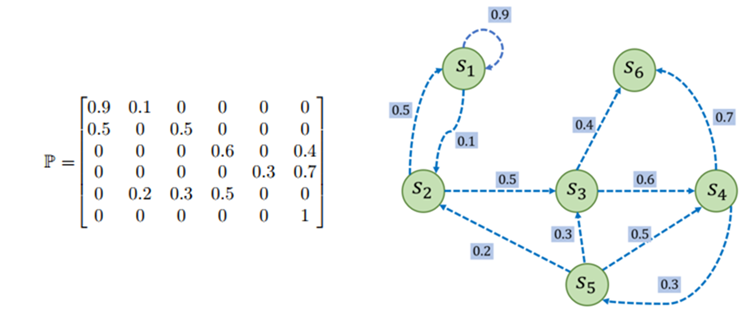
    P=[p(s1 ∣ s1)⋯p(sN ∣ s1)⋮⋮p(s1 ∣ sN)⋯p(sN ∣ sN)]\mathcal{P}=\begin{bmatrix}p(s_1\:|\:s_1)&\cdots&p(s_N\:|\:s_1)\\\vdots&&\vdots\\p(s_1\:|\:s_N)&\cdots&p(s_N\:|\:s_N)\end{bmatrix}

  • 采样（Sampling）： 给定一个马尔可夫过程，从某个状态出发并根据状态转移矩阵生成一个回合，得到对应轨迹的过程称为采样。

  • 范围（Horizon）： 一个回合的长度，每个回合最大的时间步数

    • 有限期（Infinite-horizon）： 存在终止状态，被触发后回合结束
    • 无限期（Finite-horizon）： 不存在终止状态
    • 终止状态（Terminal State）： 不在转移至其他状态的状态，可认为该状态永远转移至自身。
    • 如下图一个简单马尔可夫链例子中S6S_6为终止状态。

image-20230411113717235

MRP

  • 马尔可夫奖励过程（Markov Reward Process, MRP）： 在马尔科夫链的基础上增添奖励函数与折扣因子
    • 用四元组<S,P,r,γ><\mathcal{S},\mathcal{P},r,\gamma>表示一个MRP
  • 回报（Return）： 从当前时刻开始到本回合结束所有奖励的总和，又称累计奖励（Cumulative Future Reward）
    • 强化学习的目标为最大化回报
    • 将tt时刻回报记作GtG_t，kk步后回合结束，则回报如下表示：

Gt=Rt+Rt+1+⋯+Rt+kG_t=R_t+R_{t+1}+\cdots+R_{t+k}

  • 折扣回报（Discounted Return）： 对不同时刻奖励进行相应衰减，得到折扣回报

    • 折扣因子（Discounted Factor）： γ∈[0,1]\gamma\in[0,1]对待越久远的未来，奖励的折扣越大。

    • 使用折扣因子可使得回报能在有限步中收敛，若不用折扣因子，则无限步的回报将趋于无穷大

      Gt=Rt+γ⋅Rt+1+γ2⋅Rt+2+⋯=∑k=0∞ γkRt+kG_t=R_t+\gamma\cdot R_{t+1}+\gamma^2\cdot R_{t+2}+\cdots=\sum_{k=0}^\infty\:\gamma^{k}R_{t+k}

  • 价值（Value）： 在MRP中定义价值是回报的期望，即未来期望获得的奖励之和。

    • 所有价值构成价值函数，反映现状的好坏，价值函数越大，现状越有利。

  • 价值函数（Value Function）： 当前状态sts_t得到的期望回报V(st)V(s_t)

    • 称RtR_t为即时奖励，余下部分为未来奖励折扣总和

V(s)=E[Gt ∣ st=s]=E[Rt+γRt+1+γ2Rt+2+⋯ ∣ St=s]=E[Rt+γ(Rt+1+γRt+2+⋯ ) ∣ St=s] =E[Rt+γGt+1 ∣ St=s]=E[Rt+γV(St+1) ∣ St=s]\begin{aligned} V(s)=&\mathbb{E}[G_t\:|\:s_t=s]\\ &=\mathbb{E}[R_{t}+\gamma R_{t+1}+\gamma^2R_{t+2}+\cdots \:|\:S_t=s]\\ &=\mathbb{E}[R_{t}+\gamma (R_{t+1}+\gamma R_{t+2}+\cdots )\:|\:S_t=s]\\\ &=\mathbb{E}[R_{t}+\gamma G_{t+1}\:|\:S_t=s]\\ &=\mathbb{E}[R_{t}+\gamma V(S_{t+1})\:|\:S_t=s]\\ \end{aligned}

MRP贝尔曼期望方程

  • 贝尔曼期望方程： 定义了当前状态和未来状态间的关系，即时奖励与未来奖励折扣的和即为贝尔曼期望方程
    • 即时奖励： r(s)=E[Rt ∣ St=s]r(s)=\mathbb{E}[R_t\:|\:S_t=s]
    • 未来奖励折扣总和： 从状态s出发进行状态转移得到γ∑s′∈Sp(s′ ∣ s)V(s′)=E[γV(St+1) ∣ St=s]\gamma\sum_{s^{'}\in S}{p(s^{'}\:|\:s)V(s^{'})}=\mathbb{E}[\gamma V(S_{t+1})\:|\:S_t=s]

V(s)=r(s)+γ∑s′∈Sp(s′ ∣ s)V(s′)V(s)=r(s)+\gamma\sum_{s^{'}\in S}p(s^{'}\:|\:s)V(s^{'})

  • 矩阵贝尔曼期望方程： 若MRP存在nn个状态时，上述公式具备如下表达
    • 状态向量S={s1,s2,⋯ ,sn}S=\{s_1,s_2,\cdots,s_n\}
    • 价值函数V=[V(s1)V(s2)⋯V(sn)]T\mathcal{V}=\begin{bmatrix}V(s_1)&V(s_2)&\cdots&V(s_n)\end{bmatrix}^T
    • 奖励函数R=[r(s1)r(s2)⋯r(sn)]\mathcal{R}=\begin{bmatrix}r(s_1)&r(s_2)&\cdots&r(s_n)\end{bmatrix}

V=R+γPV[V(s1)V(s2)⋮V(sN)]=[r(s1)r(s2)⋮r(sN)]+γ[p(s1 ∣ s1)p(s2 ∣ s1)⋯p(sN ∣ s1)p(s1 ∣ s2)p(s2 ∣ s2)⋯p(sN ∣ s2)⋮⋯⋯⋮p(s1 ∣ sN)p(s2 ∣ sN)⋯p(sN ∣ sN)][V(s1)V(s2)⋮V(sN)]\begin{aligned} &\mathcal{V}=\mathcal{R}+\gamma\mathcal{P}\mathcal{V}\\\\ \begin{bmatrix}V(s_1)\\V(s_2)\\\vdots\\V(s_N)\end{bmatrix}= \begin{bmatrix}r(s_1)\\r(s_2)\\\vdots\\r(s_N)\end{bmatrix}+ \gamma& \begin{bmatrix}p(s_1\:|\:s_1)&p(s_2\:|\:s_1)&\cdots&p(s_N\:|\:s_1)\\ p(s_1\:|\:s_2)&p(s_2\:|\:s_2)&\cdots&p(s_N\:|\:s_2)\\ \vdots&\cdots&\cdots&\vdots\\ p(s_1\:|\:s_N)&p(s_2\:|\:s_N)&\cdots&p(s_N\:|\:s_N)\end{bmatrix} \begin{bmatrix}V(s_1)\\V(s_2)\\\vdots\\V(s_N)\end{bmatrix} \end{aligned}

  • 价值函数解析解： 进一步通过矩阵计算求解得到价值函数的解析解
    • 计算复杂度O(n3)O(n^3)，只适用于较小的MRP

V=R+γPV(I−γP)V=RV=(I−γP)−1R\begin{aligned} &\mathcal{V}=\mathcal{R}+\gamma\mathcal{P}\mathcal{V}\\ (I-\gamma\mathcal{P})&\mathcal{V}=\mathcal{R}\\ &\mathcal{V}=(I-\gamma\mathcal{P})^{-1}\mathcal{R} \end{aligned}

马尔可夫决策过程

MDP与策略

  • 马尔可夫决策过程（Markov Decision Process, MDP）： 在MRP的基础上增加策略（即智能体的动作）即得到MDP

    • 状态转移函数依赖于智能体采取的动作：p(s′ ∣ s,a)=P(St+1=s′ ∣ St=s,At=a)p(s^{'}\:|\: s,a)=\mathbb{P}(S_{t+1}=s^{'}\:|\:S_t=s,A_t=a)
    • 奖励函数依赖于智能体采取的动作：r(st,at)=E[rt ∣ st,at]r(s_t,a_t)=\mathbb{E}[r_t\:|\: s_t,a_t]
    • 马尔可夫决策过程由元组<S,A,P,r,γ><\mathcal{S,A,P,r,\gamma}>构成

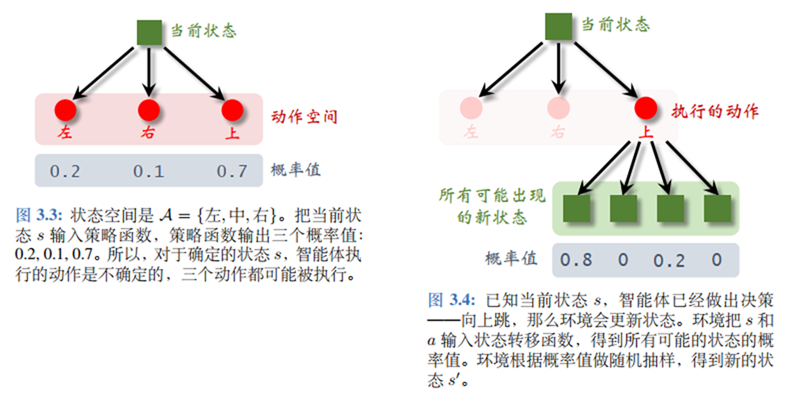
  • 策略（Policy）： 根据观测到的环境状态，智能体作出的决策，即如何从动作空间中选取一个动作。

  • 随机性策略： 随机策略将状态SS和动作AA映射至区间[0,1][0,1]，输入一个状态输出一个概率用于采样得到智能体将采取的动作：

π:S×A↦[0,1]π(a ∣ s)=P(At=a ∣ St=s)\begin{aligned} \pi:\mathcal{S}&\times\mathcal{A}\mapsto [0,1]\\ \pi(a\:|\:s)=&\mathbb{P}(A_t=a\:|\:S_t=s) \end{aligned}

  • 确定性策略： 根据环境状态，智能体直接输出最可能的动作，可视为随机策略的一种特例

μ:S↦Aμ=arg⁡max⁡aπ(a ∣ s)\begin{aligned} \mu:\mathcal{S}&\mapsto \mathcal{A}\\ \mu=\arg&\max_a\pi(a\:|\:s) \end{aligned}

image-20230411100203935

  • 智能体与环境交互（Agent Environment Interaction）： 智能体与环境存在交互
    • 智能体观测环境状态ss并根据决策π\pi作出动作aa，
    • 动作改变环境状态使其反馈给智能体奖励rr
    • 通过状态转移得到下一时刻环境状态s′s^{'}并被智能体观测到

image-20230410200519109

  • MDP转为MRP： 给定一个MDP和一个策略π\pi，可将MDP中策略的动作选择边缘化，使其变为MRP。
    • 选取动作的概率与使ss转移到s′s^{'}的概率的乘积加和，可视为MRP中的状态转移函数：pπ(s′ ∣ s)=∑a∈Aπ(a ∣ s)p(s′∣s,a)p_\pi(s^{'}\:|\:s)=\sum_{a\in \mathcal{A}}\pi(a\:|\:s)p(s^{'}|s,a)
    • 状态ss下策略π\pi选取所有可能动作aa的概率与得到的奖励的成绩加和，可视为MRP中的奖励函数rπ(s)=∑a∈Aπ(a ∣ s)r(s,a)r_\pi(s)=\sum_{a\in \mathcal{A}}\pi(a\:|\:s)r(s,a)
  • MDP同MP\MRP区别
    • 马尔可夫过程/马尔可夫奖励过程的状态转移是直接决定的，根据当前状态ss直接通过转移概率决定下一个状态是什么
    • 马尔可夫决策过程中，智能体在当前状态的时候，首先要决定采取某一种动作，随后根据智能体当前状态以及采取的动作，概率转移至后续状态

image-20230412112406879

MDP价值函数

  • 状态价值函数（State-value Function）： 遵循策略π\pi时，当前状态ss得到的期望回报Vπ(s)V_{\pi}(s)

    • 状态价值函数仅依赖于策略函数π\pi和当前状态ss，当前状态和策略越好，Vπ(s)V_\pi(s)越大

      Vπ(s)=Eπ[Gt ∣ St=s]=Eπ[Qπ(s,At)]=∑a∈Aπ(a ∣ s)⋅Qπ(s,a)Vπ(s)=Eπ[Rt+γ⋅Vπ(St+1) ∣ St=s]=∑a∈Aπ(a ∣ s)(r(s,a)+γ∑s′∈Sp(s′ ∣ s,a)Vπ(s′))\begin{aligned} V_\pi(s)&=\mathbb{E}_\pi\big[G_t\:|\:S_t=s\big]\\ &=\mathbb{E}_\pi\big[Q_{\pi}(s,A_t)\big]=\sum_{a\in\mathcal{A}}\pi(a\:|\:s)\cdot Q_\pi(s,a)\\\\ V_{\pi}(s)&=\mathbb{E}_\pi\big[R_t+\gamma\cdot V_\pi(S_{t+1})\:|\:S_t=s\big]\\ &=\sum_{a\in\mathcal{A}}\pi(a\:|\:s)\bigg(r(s,a)+\gamma\sum_{s^{'}\in \mathcal S}p(s^{'}\:|\:s,a)V_\pi(s^{'})\bigg) \end{aligned}

  • 动作价值函数（Action-value Function）： 遵循策略π\pi时，当前状态ss下执行动作aa，得到的期望回报Qπ(s,a)Q_{\pi}(s,a)

    • 动作价值函数依赖于s,as,a，当前状态和动作越好，Qπ(s,a)Q_\pi(s,a)越大

    • 动作价值函数依赖于策略π\pi，则策略越好，Qπ(s,a)Q_{\pi}(s,a)

      Qπ(s,a)=Eπ[Gt ∣ St=s,At=a]=Eπ[Rt+γRt+1+γ2Rt+2+⋯ ∣ St=s,At=a]=Eπ[Rt+γ(Rt+1+γRt+2+⋯ ) ∣ St=s,At=a] =Eπ[Rt+γGt+1 ∣ St=s,At=a]=Eπ[Rt+γVπ(St+1) ∣ St=s,At=a]=r(s,a)+γ∑s′∈Sp(s′ ∣ s,a)Vπ(s′)Qπ(s,a)=r(s,a)+γ∑s′∈Sp(s′ ∣ s,a)∑a′∈Aπ(a′ ∣ s′)⋅Qπ(s′,a′)\begin{aligned} Q_{\pi}(s,a)&=\mathbb{E}_\pi\big[G_t\:|\:S_t=s,A_t=a\big]\\ &=\mathbb{E}_{\pi}[R_{t}+\gamma R_{t+1}+\gamma^2R_{t+2}+\cdots \:|\:S_t=s,A_t=a]\\ &=\mathbb{E}_{\pi}[R_{t}+\gamma (R_{t+1}+\gamma R_{t+2}+\cdots )\:|\:S_t=s,A_t=a]\\\ &=\mathbb{E}_{\pi}[R_{t}+\gamma G_{t+1}\:|\:S_t=s,A_t=a]\\ &=\mathbb{E}_{\pi}[R_{t}+\gamma V_\pi(S_{t+1})\:|\:S_t=s,A_t=a]\\ &=r(s,a)+\gamma\sum_{s^{'}\in \mathcal S}p(s^{'}\:|\:s,a)V_\pi(s^{'})\\\\ Q_{\pi}(s,a)&=r(s,a)+\gamma\sum_{s^{'}\in \mathcal S}p(s^{'}\:|\:s,a)\sum_{a^{'}\in\mathcal{A}}\pi(a^{'}\:|\:s^{'})\cdot Q_\pi(s^{'},a^{'}) \end{aligned}

MDP预测控制

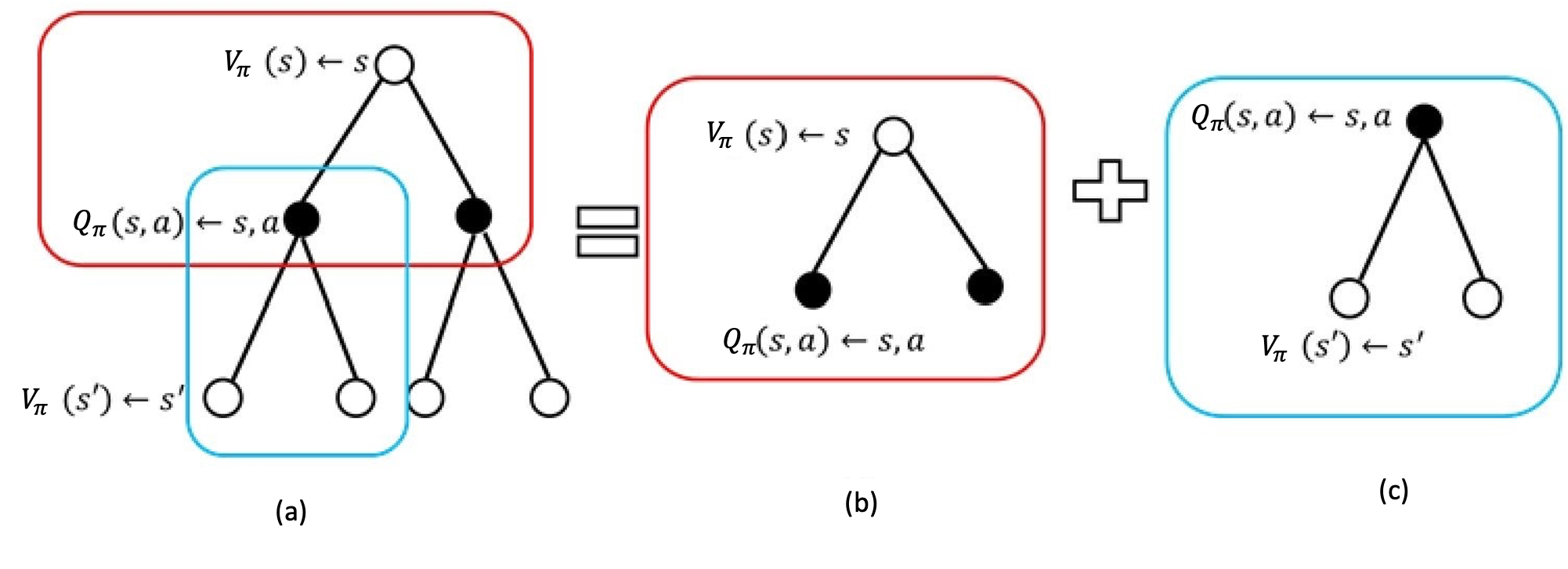
  • 备份图（Backup Diagram）： 对于某一状态，当前的价值与未来价值线性相关，采用备份图表示更新操作
    • 备份图将价值信息从一个状态（或状态-动作对）的后继状态（或状态-动作对）转移回它
    • 空心圆圈表示状态，实心圆圈表示一个状态-动作对
    • 备份图定义了未来下一时刻的状态价值函数与上一时刻的状态价值函数之间的关联

img

  • 预测（Prediction）： 已知MDP及要采取的策略π\pi，计算价值函数Vπ(s)V_\pi(s)的过程。又称策略评估

    • 预测是评估一个给定的策略，用于计算每个状态的价值
    • 输入： MDP<S,A,P,r,γ><\mathcal{S,A,P,r,\gamma }>以及策略π\pi
    • 输出： 价值函数VπV_\pi

  • 控制（Control）：已知MDP，计算最佳价值函数和最佳策略的过程

    • 控制是搜索最佳策略。并输出最佳价值函数和最佳策略的过程
    • 输入： MDP<S,A,P,r,γ><\mathcal{S,A,P,r,\gamma }>
    • 输出： 最佳价值函数V∗V^{*}和最佳策略π∗\pi^{*}
    • 最佳价值函数： 使状态价值最大的策略π\pi得到的价值V∗=max⁡πVπ(s)V^{*}=\max_\pi V_\pi(s)，最佳价值唯一存在
    • 最佳策略函数： 使状态价值最大的策略π∗=arg⁡max⁡πVπ(s)\pi^{*}=\arg\max_\pi V_\pi(s)，环境中可能存在多个最佳策略

  • 预测与控制的区分

    • MDP中使用动态规划实现预测和控制；强化学习中通过解决预测问题，进而解决控制问题

    • 预测问题给定策略，计算该策略下的价值函数

    • 控制问题不给策略，计算最佳价值函数及对应策略

img

  • 策略迭代：由策略评估和策略改进组成

    • 策略评估：给定MDP和策略π\pi（等价于MRP），求状态价值函数

      • Vπk+1(s)=rπ(s)+γpπ(s′ ∣ s)Vπk(s′)V_\pi^{k+1}(s)=r_{\pi}(s)+\gamma p_{\pi}(s^{'}\:|\:s)V_\pi^k(s^{'})
      • 迭代上式直到第k次迭代后满足收敛条件

    • 策略改进：改进上述策略，从而使得价值函数最大化

      • 根据状态价值函数推导得到Q函数（动作价值函数）
      • 使用贪心策略使得Q函数最大化：π′(s)=arg⁡max⁡aQπ(s,a)\pi^{'}(s)=\arg\max_{a}Q_\pi(s,a)
      • 迭代上式直到完成设定的迭代数或Vπ′(s)−Vπ(s)>ϵV_{\pi^{'}}(s)-V_\pi(s)>\epsilon时结束

    • 贝尔曼最优方程（Bellman Optimality Equation）： 最佳策略下状态的价值等于该状态下采取最好动作得到的回报的期望，当MDP满足贝尔曼最优方程时，达到最佳

      V∗(s)=max⁡aQ∗(s,a)π∗=arg⁡max⁡πQπ(s,a)Q∗(s,a)=r(s,a)+γ∑s′∈Sp(s′ ∣ s,a)max⁡aQ∗(s′,a′)\begin{aligned} V_{*}(s)&=\max_{a}Q_{*}(s,a)\\ \pi_*&=\arg \max_{\pi} Q_{\pi}(s,a)\\ Q_{*}(s,a)&=r(s,a)+\gamma\sum_{s^{'}\in \mathcal S}p(s^{'}\:|\:s,a)\max_{a}Q_{*}(s^{'},a^{'}) \end{aligned}

  • 价值迭代：将贝尔曼最优方程作为更新规则进行迭代，从而使得价值函数收敛

image-20230412152528551

MDP模型

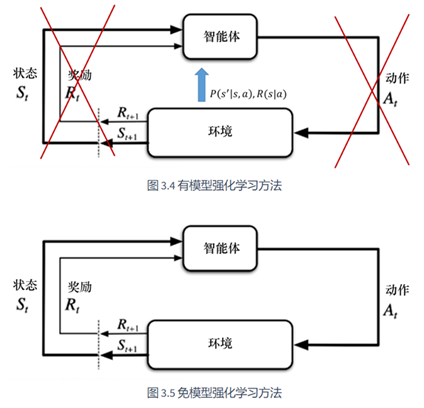
称环境为强化学习中的模型，则可将马尔可夫决策过程分为模型已知和模型未知两种：

  • 有模型： 模型已知，处于已知环境内
    • 已知环境的状态转移函数和奖励函数，称环境已知。此时采用决策的概率函数来反映环境的随机性
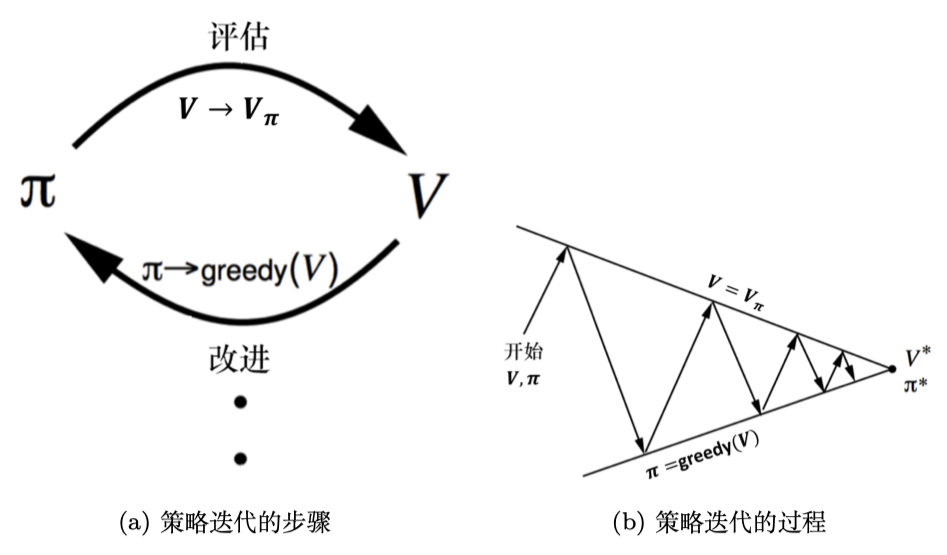
    • 通过策略迭代或价值迭代得到最佳策略
  • 免模型： 模型未知，处于未知环境内
    • 未知环境的状态转移和奖励函数，通过尝试不同的策略学习得到最好的方式
    • 使用V(s)V(s)表示状态的好坏，QQ函数判断某状态下采取什么动作能够得到最大奖励
    • 通过和环境交互学习策略

image-20230417111243093

面试题

Reinforcement Learning

Markov Decision Process